Behavior Trees as an alternative to FSM and Heirarchical FSM
Introduction
Programming robots is a tedious task and there are many moving parts that require to coordinate with each other. There are many software frameworks and best practices that are used to implement the execution of all the individual modules and interface with each other based on some conditionals. Let’s consider an example to elaborate this statement, given we have a simple robot with a depth sensor and two functionalities are implemented:
- Detect an obtacle
- Go left or right based on the free space.
Using this it has an obstacle avoidance functionality, I should also point out that there are all the system I/O calls to the hardware that have been written to formulate this solution. A simple flow chart can depict the entire functionality while abstracting out some part of the code.
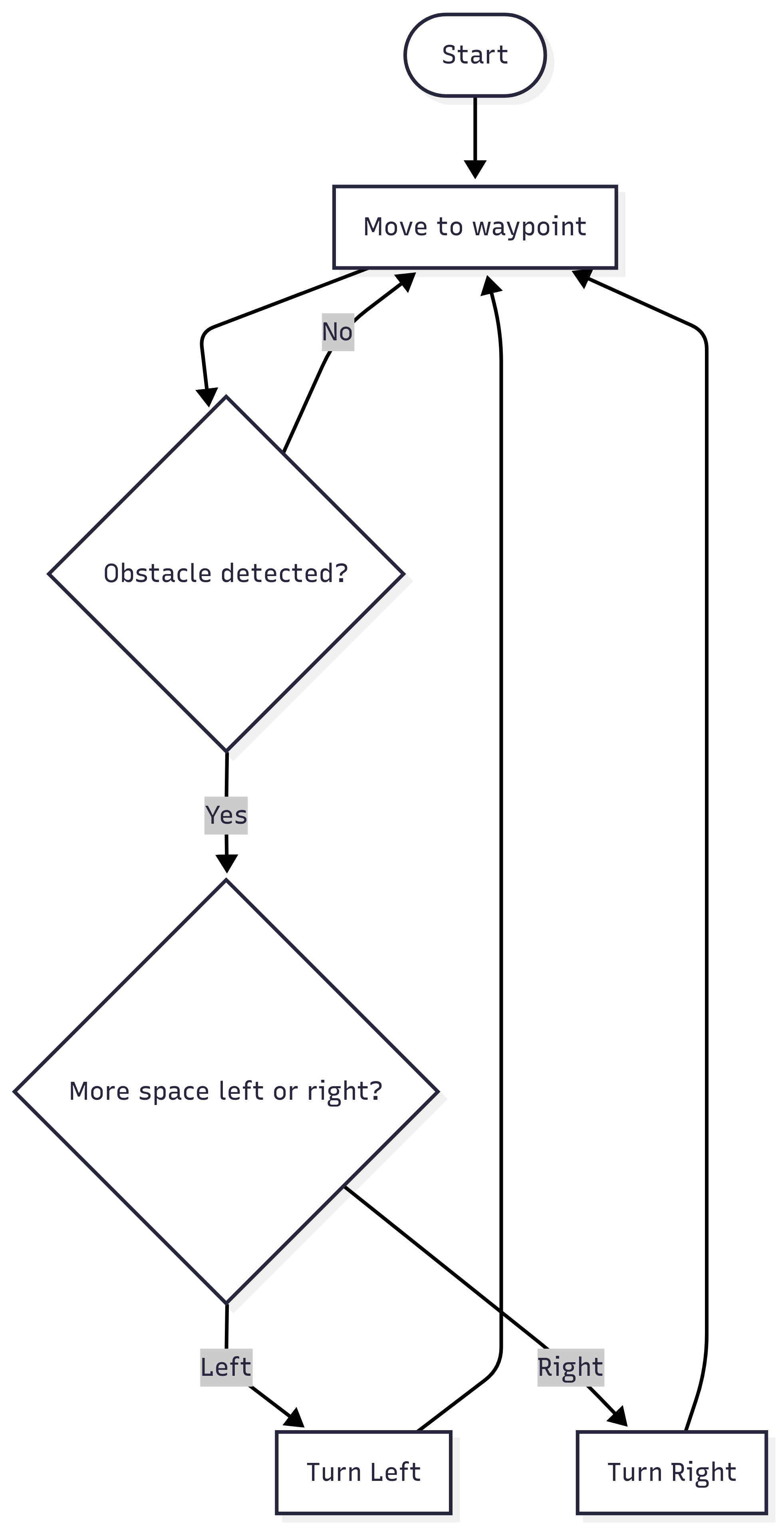
The flow chart illustrates how decisions are made based on previous inputs. Although this representation simplifies the underlying logic, it effectively conveys the sequential nature of information and data flow between components.
One could argue that this implies the system is adequately represented by a non-parallelized flow chart, although a parallel system would be a more accurate model for analysis. I will not discuss that in the current blogpost, the scope of analysing multithreaded architecture and circular buffers is beyond the topic of this post.
The flow chart above is helpful, but as any experienced robotics programmer knows, we rarely write code in chunky monolithic states. The reasons are as follows:
-
Such code is fragile to small errors, requiring many independent fallback mechanisms. And yes, bifurcations to the state machine must still be designed.
-
Low modularity reduces code usability and reusability for similar tasks across different subsystems.
-
There is minimal support for logical bug tracing. If an unexpected outcome occurs, can you reliably determine whether it was caused by extraneous factors or a bug in your code? And if it was extraneous, how many test iterations would it take to confirm that—considering each iteration consumes time, money, and effort? In most cases, I would argue no, because you cannot localize whether the logical fault occurred in the current iteration or a previous one.
Due to these reasons we use different topologies to breakdown the code or system design into simpler reusable subsystems, but different topologies have different affect on the complexity of the system, this is discussed for three major methods used in autonomy software.
Finite State Machine
These require no real introduction: a finite set of states that transition based on specific conditions or changes in state. When discussing the design of autonomous software architectures, developing individual autonomy modules and managing transitions between them is a common practice. Essentially, a finite state machine (FSM) for an autonomous system—like a robot—can be considered a hybrid automaton, i.e., a dynamical system with both discrete and continuous states.
We can attempt to model our previously defined decision system as a hybrid automaton. For example, “move left,” “move right,” and “move forward” can represent simple action states between which the system transitions.
Now, let’s evaluate how this method performs according to our earlier definition of good code:
-
There could be quick jumps between states thus not making the switches meaningful(in this case since the automata are meant for different purpose).
-
The system is modular in that individual behaviors can be written and reused elsewhere. However, its lack of robustness to rapid switching between logics means the code must account for such transitions—making it overly reliant on the structure of high-level logic, which we aimed to avoid.
-
Bug detection is relatively straightforward in small, simple logic systems. However, in larger finite automata, the number of connections between nodes increases rapidly, making it difficult to isolate the source of a bug. In highly connected architectures, identifying what exactly is failing becomes challenging. While the node that throws an error may appear to be the culprit, the actual issue might originate elsewhere—perhaps from a node that did not fail outright because the environment masked the problem. This can lead the system into an unintended state, influenced by hidden or unaccounted-for variables that begin to affect low-level control execution.
This simplistic design showed us some faults, is it possible to mitigate with better design, note that currently I am not using any slack variables, is it possible to make the structure stable? Yes a little,but adding more elements to the design adds more complexity. Generally these structures are rigid due to the high level solution they encode, and slack variables just keep adding to that complexity.
A finite state machine based architecture for mobile robots can be found in FSM’s implemented using SMACC Planner(https://github.com/robosoft-ai/SMACC).
Heirarchical Finite State Machines
A state machine of a state machine is called a heirarchical state machine, not really but now you have an intuitive understanding, they are also known as state charts. There are two main definitions required to define a heirarchical finite state machine:
- Super States: group of states that can have transitions.
- Generalised Transitions: Transitions between Super states
These new design definitions add a bit of nuance to our FSM design example by making us think of things that can be clubbed together. A clear way to do this is by clubbing move left and move right together into move away and we can rewire to show it as shown in the figure:
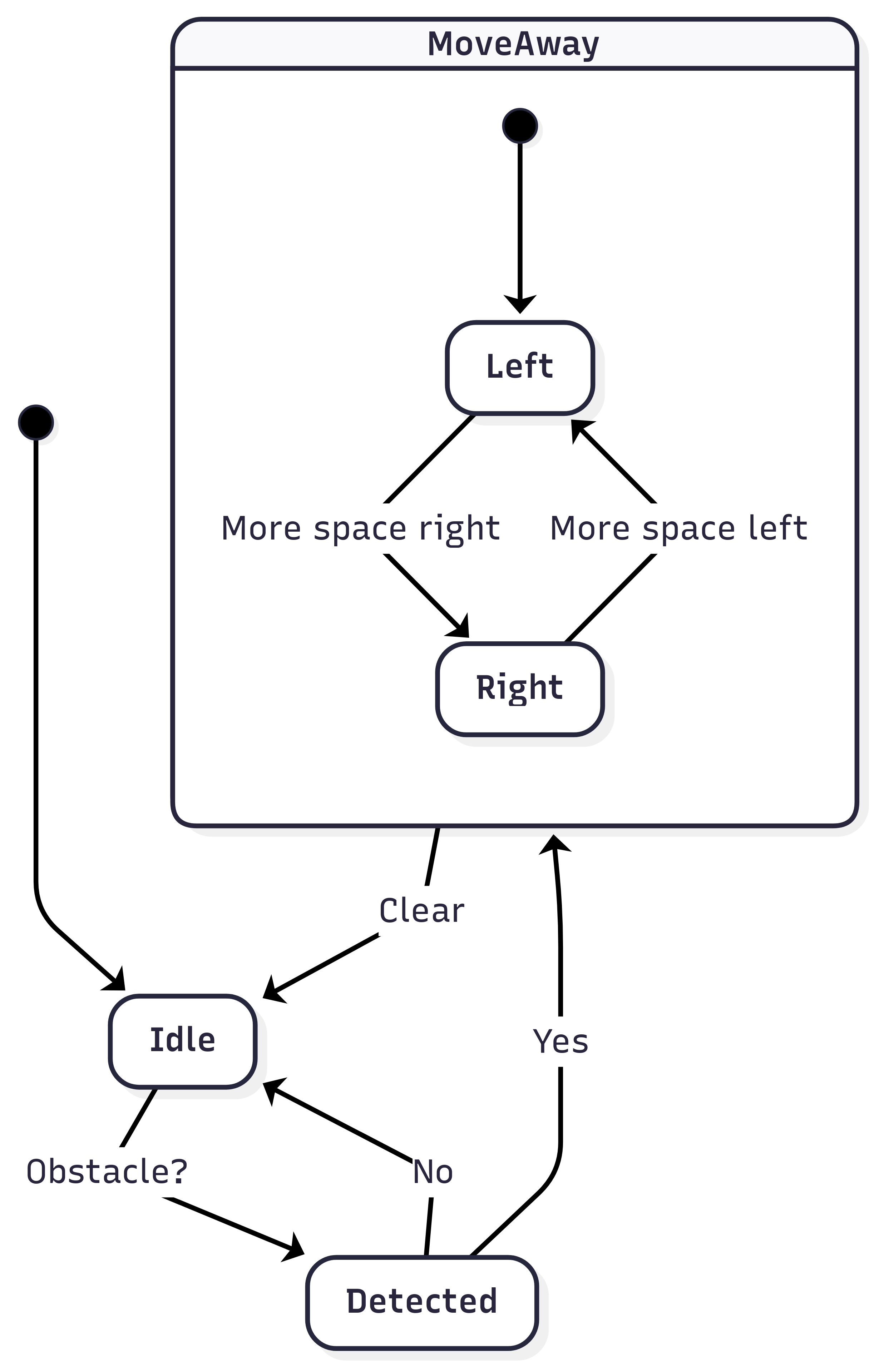
This resolves the complexity a little bit, but remember this is a statechart design from a state machine i.e. bottom-up design and not a top to bottom design i.e. we didn’t design the behavior and move to the atomic parts. Doing it that way, we can have many ways to model this behavior.
Now we judge HFSM based on our three parameters, namely complexity, bug finding and code modularity. Let’s see them one by one on how they perform on these metrics:
-
Bug finding remains tough, given there may not be a set sequence in which the states execute, it is possible to get caught in loops, and if an error occours in time, it becomes difficult to isolate the state/hyperstate that caused this issue.
- Code modularity depends on the type of approach considered while designing the overall system. We discuss this in context of two design approaches to design state charts:
-
If the approach considered is bottom-top then it is possible that high level behaviors are not re-usable since they will be made with some patches in addition to the core low level module, for eg. move straight and turn right would differ in small patch work of what kind of input they take and the way they interact with the outputs, why so? because the two things differ at the physics level, as in giving velocity and accelaration information becomes relevant for a right turn but may not be as relevant for a move straight, still relevant but not essential as compared to other. This makes the two subsystems to look different and making the system more complicated as we get into higher level design.
-
Top-bottom level design mitigates these issues to a large level, and modules are thought as members that need to exist but nothing explicitly is stated unless top level connections are not fixed. Once we fix top level connections we can get into designing low level specific modules. Reusability of modules can be decided on the level of abstraction, you get this choice in only top to bottom design scheme, in bottom to top you just can’t do this since, you don’t know what a top level architecture looks like so atomic design doesn’t suit the overall architecture.
-
-
It is worth mentioning in top to bottom design you need to stop at some level of abstraction to design low level modules so that you can make design optimisations if required for performance. Since, after a point the high level specification of the robot are catered to and we need optimisation to match specifications of the product/API.
- An extra point worth mentioning as also done in this blog is that designers often find really meaningful edge cases while designing state charts. This is obvious when we look at our above discussion, thinking in a top-down fashion makes you think of all the big picture challenges and then designing behaviours become part of a robust behavior planning procedure during the on paper design, though this will add considerable time and testing apparatus(time and resources), but the design becomes robust.
Based on these it is easy to conclude that overall we have a much better system than vanilla FSMs but these may or maynot be good for real time systems, for event driven systems that are non-autonomous they work good, this can be seen from emperical experience of UI designers evidence 1, evidence 2. Evidence 2 is stateflow designer for people who develop MATLAB programs.
Behavior Trees
The connection between these behaviors is based on different kinds of nodes like switching nodes (selectors), sequential nodes (sequences), and decorator or condition nodes which allow us to guide execution in a flexible and intuitive manner. The behavior tree structure resembles a directed rooted tree where control flows from the root node down through its children. Execution propagates depending on the status of each node — which can be SUCCESS, FAILURE, or RUNNING.
Each node behaves in a well-defined manner:
- Sequence nodes proceed through children until one fails.
- Selector nodes try children until one succeeds.
- Decorator nodes modify the result of their child (like retrying or inverting result).
- Action/Leaf nodes perform specific tasks (e.g., “Turn Left”, “Wait”, “Publish Message”).
This allows a natural and readable encoding of high-level behavior while still preserving execution safety and debugging granularity.
Let’s now consider an example from the Behaviortree-rca repository. The bt_rca tree (used for rule-based RCA logic) and the bt_nav tree (used for navigational behaviors) illustrate the structure and strength of this approach.
Example from the Repository: RCA Behavior Tree
In the bt_rca.xml file, we define a set of actions and conditions that help the robot debug or recover from various failure modes (root cause analysis). Here’s a fragment:
<BehaviorTree ID="RCA_Tree">
<Sequence name="root">
<Condition ID="is_nav_stuck"/>
<Selector name="rca_selector">
<Sequence name="recovery_strategy_1">
<Action ID="ClearLocalCostmap"/>
<Action ID="RetryNavigation"/>
</Sequence>
<Action ID="NotifyOperator"/>
</Selector>
</Sequence>
</BehaviorTree>
In plain English, this says:
- If navigation is stuck (
is_nav_stuckreturns SUCCESS), - Then try a sequence of recovery strategies:
- First try clearing the local costmap and retrying navigation.
- If that fails, notify the operator.
Unlike FSMs or HFSMs, there’s no need to encode transitions explicitly — they are implicit in node status. And new strategies can be appended without disrupting the existing logic.
Example from the Repository: Navigation Behavior Tree
The bt_nav.xml defines the core navigation behavior using NavigateToPose, Wait, and utility actions. Here’s a simplified snippet:
<BehaviorTree ID="NavigateWithWait">
<Sequence name="navigate_sequence">
<Action ID="CheckBatteryLevel"/>
<Action ID="NavigateToPose"/>
<Decorator ID="RetryUntilSuccessful" max_attempts="3">
<Action ID="Wait"/>
</Decorator>
</Sequence>
</BehaviorTree>
This tree:
- Checks if the battery level is sufficient before navigation.
- Navigates to the target pose.
- If that fails or returns RUNNING, it waits and retries up to three times.
Again, the design here shows how fault-tolerance and fallback behaviors are trivially implemented using standard tree structures.
Benefits Recap
Judging Behavior Trees against our earlier metrics:
- Modularity: Each subtree (like “NavigateToPose” or “ClearLocalCostmap”) is a modular unit of behavior, easily testable and swappable.
- Debuggability: Tree visualization tools like Groot make it easier to follow and debug execution flow live.
- Reusability: Once a subtree is defined and tested, it can be reused in multiple trees or composed into more complex behaviors without altering its internal logic.
Furthermore, BTs shine in real-time systems. Unlike FSMs, they naturally allow concurrent checks and actions using parallel nodes, enabling dynamic responsiveness without state explosion.
Conclusion
Behavior Trees offer a scalable, modular, and robust alternative to traditional FSMs and HFSMs for autonomous robotic task execution. They encourage top-down design, improve reusability, and enable fine-grained debugging, all while keeping the execution structure readable and maintainable.
If you’re building ROS-based robots and struggling with stateful logic using FSMs or bespoke event graphs, Behavior Trees (especially with plugins like BehaviorTree.CPP) might be the toolchain upgrade you need. I invite you to explore the Behaviortree-rca repository and try writing your first tree. It’s surprisingly intuitive once you start.
Appendix: A more Mathematical Definition and approach to Finite State Machines
A mathematical definition of the finite state machine would be given by a triplet (L,A,E). Where L is the finite set called the state-space, A is the finite set called the alphabet whose elements are called symbols. E is the transition rule; it is a subset of LxAxL and its elements are called edges(or transitions or events)
A Deterministic input-output automata can be represented by equations of the following form: \(l^{\#} = \nu(l,i) o = \eta(l,i)\)
where \(l^{\#}\) denotes the new value of discrete state after the event takes place, resulting from the old discrete state value l and the input i.
A set valued mapping from \(\mathbb{R}^{m}\), or from a subset S of \(\mathbb{R}^{m}\), associates, with every point \(x \in \mathbb{R^m}\), or every point \(x \in S\), a subset of \(\mathbb{R}^{n}\). It’s notation is double arrow, \(M: \mathbb{R}^{m} \rightrightarrows S\), for \(S \in \mathbb{R}^{n}\), indicates that M is a set valued mapping with \(M(x) \in S\) where S is a subset of \(\mathbb(R)^m\).
A hybrid system can thus be defined using 4 elements:
- a set \(C \in \mathbb{R}^n\), called the flow set
- a set valued mapping \(F: \mathbb{R}^n \rightrightarrows \mathbb{R}^n\) with \(C \in dom(F)\), called the flow map;
- a set \(D \in \mathbb{R}^n\), called the jump set;
- a set-valued mapping \(G: \mathbb{R}^n \rightrightarrows \mathbb{R}^n\) with \(D \in dom(G)\), called the jump map;
A hybrid dynamical system can be represented by the notation H = (C,F,D,G). This can be simplified a bit more but I’ll post a tutorial on hybrid dynamical systems and that’ll have more mathematical content on this topic, with examples. For now this shall do for an intuition on what is going on in a robot and what the model of software running on top of it, should look like.